
Stray light and the effect it has on Optical Signal to Noise ratio (S/N) falls into one of two major categories: a) random scatter from mirrors, gratings, etc., or b) directional stray light.
杂散光和它对光学信噪比(S/N) 的影响可以分为两大类:a) 来自反射镜、光栅等的随机散射;b) 反射、二次进入信号、光栅鬼线和光栅生成的聚焦杂散光这些现象造成的直接杂散光。
首先考虑待测量的主要波长上有多少光信号,然后和其他可能产生散射信号的波长相比较。
随机杂散光的强度正比于散射光学元件上单位面积的信号流。为计算由于随机散射产生的杂散光:
假定G= 光栅和探测器之间的光展量。
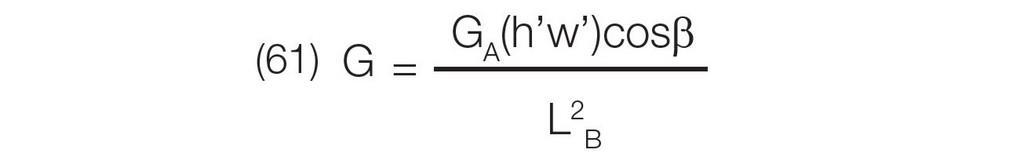
令 Bd = 杂散光的辐射度,与总信号流密度 ΦT/GA成正比。
C = 表示与随机散射有关的光学元件(包括光栅)质量因子。

总的散射流正比于散射光的辐射度、入口狭缝的开口面积以及出口狭缝对探测元件的立体角。随机通量由下式给出:Φd = BdG
然后,
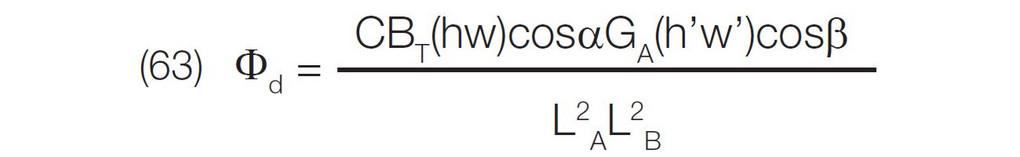
待测波长上的信号流Φu与随机信号流Φd之比为:

优化包含两部分内容:(Φu/Φd) 的最大化和杂散反射的消除。逐一考虑式(63) 中的各项:
C:尽可能采用高质量的光学元件,比如采用全息光栅。
Eλ:保证光栅在待测波长上衍射效率最优。
L2A/(hw):很不凑巧,这一参数不是完全自由的,因为还要考虑色散值和光谱带宽的要求。
Tgλ:像在垂直色散面方向的放大主要决定于散光偏差。现在的问题是,需要增加出口狭缝高度来收集所有的光信号,但是同时带来光学信噪比的损失。现在,某些CZ 型光谱仪中采用新型像差校正平面光栅,来减小散光误差,增加信噪比。
Bλ/BT:这一项代表待测波长上的强度与光源的总强度之比。这通常是使用者无法改变的。
这是一项寻找平衡点的实践。比如说,有一名研究人员,手上有一台焦距500 mm 的单色仪,但是他对信噪比不满意。式(64) 提示可以采用更长焦距的仪器来改进信噪比;假定恰好有一台焦距1000 mm 的光谱仪可以利用。假定两台仪器上的实验对光谱带宽的要求相同,光栅刻线密度、波长效率优化和光栅的面积都相同,但是结果是光通量却减小一半(根据式( 52 ),其他的参数均相同的情况下,光展量反比于焦距)。
光学信噪比参数将增加为2 倍。参看式(64),焦距的平方项使得信噪比增加为4倍,另外由于狭缝高度相同而焦距1000 mm系统上的狭缝宽度比焦距500 mm系统上的狭缝宽度宽一倍,从而使得信噪比减小为1/2。这名研究人员面临的问题是,是否值得损失光通量的一半来实现信噪比的2 倍增加。在这个实例中,Tg的值可能也会减小,原因在于散光偏差正比于数值孔径(上述情形中散光偏差相比焦距500 mm的系统可能会成倍增加)。
而且,寻找一个灵敏度更高的探测器也是值得考虑的方案。通常,小尺寸探测器会比大尺寸探测器具有更高的灵敏度。否则,光通量的减少可能会带来与预想大相径庭的结果。
如果光束大小超过光学元件的大小,将会带来一系列杂散反射,比如来自反射镜支架、固定螺钉或者是阳极电镀处理过的外壳发出的荧光。解决方案很简单:精心设计入口光学部分来优化系统的光展量,并采用场透镜使得开口阻挡(瞳孔) 相匹配。这一思路是这样实现的:通过入口狭缝处的“现场”透镜将入口光学的开口阻挡成像在光谱仪的开口阻挡(通常是光栅) 处,然后通过位于出口狭缝处的场透镜将光栅成像在出口光学的开口阻挡处。
In some CZ monochromator configurations, a diffracted wavelength other than that on which the instrument is set may return to the collimating mirror and be reflected back to the grating where it may be rediffracted and find its way to the exit slit.
在一些CZ 型单色仪中(特别是采用低刻线密度光栅工作在可见或者紫外波段的情况),一个非待测波长上的信号可能会回到准直反射镜并反射回到光栅,然后它再次衍射并到达出口狭缝。如果这个问题很严重,一个有效的解决方法是在垂直光栅并经过光栅中心的平面上放置与狭缝具有相同高度的遮挡物。如果知道准确的波长,那么可以计算这一反射波长在光栅上的位置。此时,只需要对光栅上的这个点实施遮挡。
这一类实例在很多光谱仪(与类型无关) 采用线阵或者矩阵探测器时常出现,重新反射并回到光栅的情况很严重。解决方法是倾斜阵列探测器直到分辨率开始降低,或者对系统的设计进行改进,如光谱仪的非对称式设计(比如HORIBA科学仪器部的iHR320/iHR550 光栅光谱仪的非对称式光路设计,光路设计经过计算机模拟,优化和确定光学元件位置,精确消除二次衍射光)。
刻划光栅会出现鬼线和杂散光,他们会聚焦在色散平面上从而无法补救,除非采用另一块性能更好的光栅。最好的解决方法之一是采用离子刻蚀闪耀全息光栅,它提供待测波长上最好的衍射效率,而且没有任何鬼线。任何残余杂散光将被随机散射,从而无法聚焦。
这一节主要分析狭缝尺寸对信噪比在光源是连续谱或者单色光时的影响,分别考虑单级和双级单色仪两种情形。假设入口和出口狭缝的尺寸是匹配的。
观察结果:信噪比不随狭缝宽度变化。
分析:根据式(52)信号输出随着狭缝宽度的平方增加( 狭缝宽度决定入口光展量和光谱带宽)。由于光源是连续谱,因此信号随着光谱带宽和光展量的增加同时增加。“噪声信号”也随着狭缝宽度的平方增加,如式(63)所示。因此,信号和噪声都以相同的系数变化。
观察结果:信噪比与狭缝高度成反比。
分析:信号输出随狭缝高度线性变化(根据公式 ( 52 ))。然而,噪声却随着狭缝高度的平方变化(根据方程(63))。因此,信噪比随狭缝高度反比变化。
观察结果:信噪比随狭缝宽度反比变化。
分析:信号输出随狭缝宽度正比变化(即使光谱带宽增加,也只有光展量决定入射的光子数目)。“噪声”正比于狭缝宽度的平方。因此,信噪比随狭缝宽度反比变化。
观察结果:信噪比随狭缝高度反比变化。
分析:信号输出随狭缝高度线性变化。噪声随狭缝高度的平方变化。因此,信噪比随狭缝高度反比变化。
观察结果:信噪比随狭缝宽度反比变化。
分析:信噪比在第一级单色仪出口处不随狭缝宽度变化,然而,此时第二级单色仪的输入光相当于单色光,因此,信噪比随狭缝宽度成反比变化。
观察结果:信噪比随狭缝高度的平方反比变化。
分析:第一级单色仪出口处信噪比随狭缝高度反比变化。当输入光为“单色光”时,第二级单色仪的信噪比同样也随狭缝高度反比变化。因此,总的信噪比随狭缝高度的平方反比变化。
观察结果:信噪比随狭缝宽度的平方反比变化。
分析:第一级单色仪出口处信噪比随狭缝宽度反比变化。当输入光为“单色光”时,第二级单色仪的信噪比同样也随狭缝宽度反比变化。因此,总的信噪比随狭缝宽度的平方反比变化。
观察结果:信噪比随狭缝高度的平方反比变化。
分析:每一级单色仪出口处信噪比随狭缝高度反比变化,因此,总的信噪比随狭缝高度的平方反比变化。
如您有任何疑问,请在此留下详细需求信息,我们将竭诚为您服务。