
流量:流量(flux)为单位时间内通过的能量(单位是光子数/秒,或者瓦),即从光源或者已知面积的狭缝以立体角(Q)发出、在某一波长(或者某一光谱段)上的光信号。
强度 (I):在某一波长(或者某一光谱段)上单位立体角内流量的分布(单位是瓦/球面度)。
辐射度 (流明度) (B) :在一已知面上的强度。也定义为B=强度/光源的表面积(单位是瓦/球面度/cm 2)。
Typical Monochromator System.
S = 光源面积
S' = 入射狭缝面积
S" = 反射镜 M1 面积
S* = 出口狭缝面积
Ω = L1处收集光的半角
Ω' = L1处出射光的半角
Ω" = M1处收集光的半角
Ω* = M2处出射光的半角
L1 = 用于收集来信号光的透镜
M1 = Czerny-Turner结构中的球面准直反射镜
M2 = Czerny-Turner结构中的球面聚焦反射镜或超环面镜
AS = 光开口阻挡
LS = 透镜L1上有光信号通过的区域
p = 物(光源)到透镜 L1 的距离
q = 入口狭缝处的像到透镜L1的距离
G1 = 衍射光栅
几何光展量(几何延伸量)G,可以用光学系统收集光信号的能力来表示。它是发射源其面积S和光信号传播的立体角Q这两个参数的函数。因此,光展量是影响系统光通量的因素。
(40) d 2 G = dS.dQ
(41) G = ∫∫ dS.dQ
沿光线传播的圆锥角积分,该圆锥的轴线垂至于光源表面(见图 30)。
(42) G = πΣsin 2 Ω
光展量是系统的不变参数,由整个光学系统中展量最小的部分决定。几何光展量可看作是系统能够接收的最大光束大小,因此,有必要从光源开始保证系统中任何辅助光学元件都能够收集和传播最大数目的光子。
根据式(42),满足以下条件时光展量能够被最优化
(43) G = πSsin 2 Ω = πS'sin 2 Ω' = πS ”sin 2 Ω”= πS*sin 2 Ω*
当光谱仪的f数慢于f/5时(f/6、f/7等),可以采用以下更简化的近似。
(44) G ≈ S x Q
(45) Q= LsP2
因此,代入式(44)得到:
当满足tanΩ≈sinΩ≈Ω(弧度)时,这一近似非常准确。当f数为f/5时,误差约为1%,而当f数为f/1时,误差约为33%。因为数值孔径=μsinΩ=NA,因此:
(47) G ≈ π S (NA) 2
这个等式对于光纤光学和显微镜物镜的相关计算非常实用。
h = 入口狭缝的高度 (mm)
w = 入口狭缝宽度,光谱带宽/色散值 (mm)
F = 焦距长度 LA (mm)
n = 光栅的刻线密度 (g/mm)
GA = 光栅的使用面积 (mm2 )
Sg = 光栅使用区域的投影面积 = GA x cosα(mm2 )
k = 阶次
BP = 光谱带宽 (nm)
SES = 入口狭缝的面积 (mm2 )
入口狭缝的面积 SES = w ╳ h(参考方程(37)),其中:

所以,

计算光展量 G,
(50) G ≈ S ES x Q
且
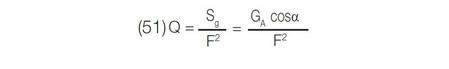
然后
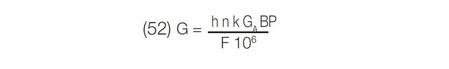
因此,系统的相对光通量正比于:
理论上,h/F因子的存在意味着可以通过增加入口狭缝的高度来提高光展量。然而实际中,这将会导致杂散光的增加,而且还会导致系统成像偏差的劣化从而减小分辨率和光谱带宽。
光流量等于辐射度和光展量的乘积
(53) Φ = B x G
(54) Φ = B π S'sin 2 Ω'
其中,B是光源参数的函数,S'是入口狭缝(或者发射光源)的面积,而Ω是光束在光谱仪入口狭缝处的半圆锥角。
由于在没有其他损耗的情况下,光流量、光展量和辐射度必须在物和像之间守恒,因此上述这些是我们用来计算理论最大光通量的全部所需参数。
首先,计算光源的光展量:
光纤的芯径为50 μm,产生的光束其数值半径NA =0.2。那么光纤的通光面积为:
(55) S = πr 2 = π(0.025) 2 =1.96×10 -3 mm 2
然后
(56) G = πS(NA) 2 = π(1.96×10 -3 )(0.2) 2
因此,光源的光展量 G = 2.46 × 10-4
下一步,计算光谱仪的光展量,假设500 nm处的光谱带宽为0.5 nm:
n = 1800 g/mm (已知)
k = 1 (已知)
DV = 24° (已知)
LA = F = LB = 320 mm (已知)
GA = 58 × 58 mm 光栅的刻划面积 (已知)
α500nm = 15.39°(根据式(19))
β500nm = 39.39°(根据式(2))
f/光谱仪的值 = f/5(根据式(28))
光谱仪的 NA = 0.1(根据式 ( 21 ))
f/光纤值 = f/2.5(根据式(21))
光纤的 NA = 0.2(已知)
h为待求参数。
计算所需设定的狭缝几何参数:
狭缝宽度,w,根据式( ( 48 )有

从 ( 32 ) 得到出口狭缝宽度 = w = 0.3725 mm
在这种情况下,我们将入口狭缝高度和出口狭缝高度设置为 0.2987 mm。
光谱仪的光展量由式 ( 52 ) 给出。
然后,
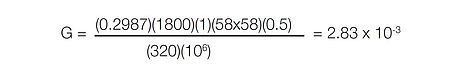
因此,光源的光展量 (2.46 × 10 -4 ) 远小于光谱仪的光展量 (2.83 × 10 -3 )。
如果光纤只是简单地放置在入口狭缝中间,数值孔径0.2的光纤与数值孔径0.1的光谱仪之间的不匹配(从f/2.5到f/5),将导致光子损失和杂散光的产生。在这种情形下,系统的光展量将由光纤纤芯的面积和光谱仪的数值孔径共同决定。
现在的关键点是对光纤发出的光进行重新成像,使得光纤的光展量增大并和光谱仪保持一致,以便所有的光子都能够进入光谱仪并传播。
可以在光纤光源和光谱仪之间加入辅助的光学元件来实现这一功能,如下:
(NA)in = 光纤的数值孔径
(NA)out = 光谱仪的数值孔径
然后:
G = πS (NA) 2输入= nS'(NA) 2输出
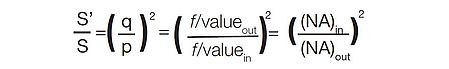
并且
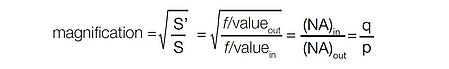
薄透镜方程为
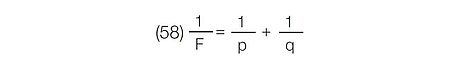

在这种情况下,F是无限远物体的焦距,p和q是有限物体和图像坐标。以直径为60 mm 的镜头为例,其中F = 100 mm,
然后:

代入方程 (58)
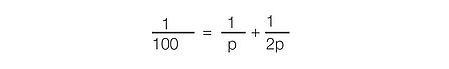
求解得到,p = 150 mm 和q = 300 mm。又有,
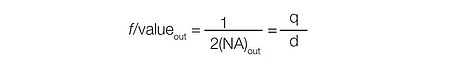
求解得到,p = 150 mm 和q = 300 mm。又有,
那么 d = 150 × 0.4 = 60 mm。
因此,从光纤发出的光被透镜以150 mm物距(p)接收,光纤纤芯的像投射到距离透镜300 mm(q)的光谱仪入口狭缝处。光信号从光纤到光谱仪的传播,均保证f数的匹配。然而,像被放大2倍。
考虑到我们为了得到0.5 nm的光谱带宽,设置的入口狭缝宽度为0.2987 mm,而光纤纤芯的像大小为100 μm,小于狭缝宽度,因此,这些设置保证了所有的光信号均能够被系统接收和传播。令人感兴趣的是,由于光纤纤芯的像小于狭缝宽度,因此,光谱带宽将由像本身来决定。减小狭缝宽度使它和光纤纤芯的像恰好匹配能够最大限度地抑制杂散光。
所谓“宽光源”是指光源本身的尺寸比实现一定光谱带宽所需的狭缝宽度还要大。在这种情形下,光谱仪的光展量要小于光源的光展量。
以汞灯作为宽光源的实例来讨论,其光展量的计算如下:
光源的面积 = 50 mm (高) ×5 mm (宽) (已知) = 250mm2
Ω= 90°
然后,G = πS sin2Ω= π250 sin290°= 785.4
假设采用与光纤光源实例 ( 43 ) 中的相同的光谱仪和光谱带宽要求,狭缝宽度和光谱仪的光展量也都保持不变。然而,光源的光展量却非常大(与光源的光展量相比,光谱仪的光展量只有2.8 × 10 -3,远远小于785)。
由于系统的光展量是由光展量最小的那部分决定的,因此,对光源的最大收集能力取决于光谱仪的光收集能力。在上一个实例中,入口狭缝的高度(h)设置为0.2987 mm。然而,对于宽光源,需要采用更大的狭缝高度,因此我们设置入口和出口的狭缝高度为3 mm (也可以采用更大的狭缝高度,但是杂散光水平直接正比于狭缝高度)。
因此,光谱仪的展度从 4.7 × 10-3增加到 4.7 × 10-2。
这一结果是系统的有效光展量值将决定对光源的光收集效率。最好的办法是在汞灯上选择一部分和入口狭缝面积大小相等的区域,把这一区域成像在入口狭缝处,而且保证其立体角等于由衍射光栅决定的立体角(式(51))。
为了计算入口处光学元件的几何参数,以上一个实例中用到的直径60 mm、焦距100 mm的透镜为例。
我们知道,在这一情况下入口狭缝的尺寸决定了光源被取样部分的面积,因此,SES=光源S的面积。
光源必须1:1成像在入口狭缝处,因此,放大倍数=1。
根据薄透镜方程:
其中

p = 2F 且 q = 2F
因此,汞灯需要放置在离透镜L1 200 mm的位置,而同样离入口狭缝的距离也是200 mm。
下一步根据光谱仪的f 数=5计算所需的透镜直径,以得到正确的f 数。
我们得到,d = 200/5 = 40 mm。
因此,直径60 mm的透镜,需要被挡住一部分而成为直径40 mm的透镜,来得到进入光谱仪的光束最佳立体角。此时,整套系统将在最大光收集的条件下工作。
假设:光源的像大小大于入口狭缝大小。
wi = 初始入口狭缝宽度(例如,100 μm)
wo = 出口狭缝宽度(入口狭缝像的初始宽度,例如,110 μm)
A tungsten halogen lamp or a spectrum where line widths are significantly greater than instrumental bandpass (this is often the case in fluorescence experiments).
比如说,卤钨灯或者是一条线宽远大于仪器带宽的谱线(荧光实验常常是这种情况)。
光通量会随着光谱带宽和光展量的乘积改变。
情况1:将入口狭缝宽度wi扩大为两倍,但是保持出口狭缝不变,我们得到:
入口狭缝宽度 = 2wi (200 μm)
出口狭缝宽度 = wo (110 μm)
光展量保持不变(决定于出口狭缝)。
光谱带宽增加为两倍。
光通量增加为两倍。
情况2:将出口狭缝宽度wo扩大为两倍,但是保持入口狭缝不变,我们得到:
入口狭缝宽度 = wi (100 μm)
出口狭缝宽度 = 2wo(220 μm)
光展量保持不变(决定于入口狭缝)。
光谱带宽增加为两倍。
光通量增加为两倍。
提示:将出口狭缝宽度增加为两倍使得更宽的一段光谱通过出口出射,从而增加了光子流。
情况3:将入口、出口狭缝宽度均扩大为两倍,我们得到:
入口狭缝宽度 = 2wi (200 μm)
出口狭缝宽度 = 2wo (220 μm)
光展量增加为两倍。
光谱带宽增加为两倍。
光通量增加为四倍。
A light source that will produce a number of monochromatic wavelengths is called a discrete spectral source.
产生一系列单色波长的光源被称为离散光谱光源。
实际情况中,单色线光源通常是连续谱的离散部分。假设谱线本身的线宽小于仪器能够达到的最小光谱带宽。
光通量随光展量变化,而与光谱带宽无关。
情况1:将入口狭缝宽度wi均扩大为两倍,但是保持出口狭缝不变,我们得到:
入口狭缝宽度 = 2wi (200 μm)
出口狭缝宽度 = wo (110 μm)
光展量保持不变(取决于出口狭缝)
光谱带宽增加为两倍
光通量保持不变
情况2:将出口狭缝宽度wo均扩大为两倍,但是保持入口狭缝不变,我们得到:
入口狭缝宽度 = wi (100 μm)
出口狭缝宽度 = 2wo (220 μm)
光展量保持不变(取决于入口狭缝)
光谱带宽增加为两倍
光通量保持不变
提示:对于离散光谱光源,将出口狭缝扩大为两倍并不能增加光通量,因为这并没有增加仪器的光子流。
情况3:将入口、出口狭缝宽度均扩大为两倍,我们得到:
入口狭缝宽度 = 2wi (200 μm)
出口狭缝宽度 = 2wo (220 μm)
光展量增加为两倍
光谱带宽增加为两倍
光通量增加为两倍
如您有任何疑问,请在此留下详细需求信息,我们将竭诚为您服务。