
Schematic image of the tip-in and the tip-out, showing the localization of the field enhancement with respect to the diffraction limited size of the excitation laser (left), and schematic sketch of the near-field and far-field probed volumes.
TERS实验中拉曼信号获得放大的主要原因是TERS针尖附近的电磁增强(EM)。这一节我们将介绍在TERS研究人员中广泛采用的基本计算公式。
为了计算增强因子 (enhancement factor,EF),需要用到以下变量的数值:
一般来说,增强因子EF的估算可以理解为纯近场成分与远场成分之比,EF可以表示为23:
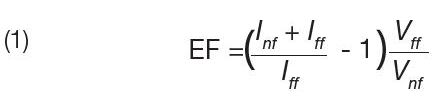
上述公式中,Inf 和 Iff 分别是来自于近场和远场成分的拉曼散射强度,括号中的表达式代表强度对比 (近场贡献与远场贡献的比值),源于图 9-8 中所显示的针尖“在位” 和“离位”两种情况下的拉曼强度,Vff 和Vnf分别是近场和远场情况下探测的体积。这一计算的前提是假定来自于样品表面的远场拉曼信号无论针尖“在位”和“离位”时都保持在焦点区域内。
远场强度Iff是 TERS 针尖退出 (“离位”)时测得的,其信号来自于焦点附近体积Vff:

上式中,Rfocus 和 hff 分别是焦点处激光束的半径和有效聚焦深度。
Comparison of focus spot objective lens assigned from top with 0 degree relative to orthogonal plane with sample plane and with 60 degree.
另一方面,当针尖紧邻样品表面 (1-3 nm) 时,采集到的拉曼强度同时包括近场和远场的贡献,表示为Inf + Iff 值得注意的是,对于直径小于20 nm的针尖,可以认为远场的贡献也来自于针尖自身的镜像效应,则全部场的贡献可以看作是Inf +2 Iff24
探测到的近场信号 Inf 来自于 TERS 针尖尖端周围很小的一块体积,这块TERS体积可以定义为 π(RTERS)2hnf,其中RTERS 和 hnf分别是近场的半径和有效高度。为了估算近场半径,可以做以下近似:RTERS ≈ ½ Rtip,当 TERS 实验是在倾斜反射模式下进行,入射光与样品表面之间的入射角不等于零时,焦斑形状为椭圆形,其数值可以表示为直射焦斑大小除以cosα,α 是倾斜角,如左下图所示,椭圆形状影响到了作用在针尖上的聚焦强度。
Comparison of a Far-Field Raman scattering spectrum with the Tip-Enhanced Raman spectrum of Azobenzene molecules grafted on a flat gold film.
但是实际中记录到的远场拉曼强度受这一焦斑尺寸的增大的影响很小,其中原因是光场强度下降这一因素得到了椭圆区域内探针分子个数更多这件事的补偿。
当样品足够薄时,近似地有hff ≈ hnf,以上公式(1)可以进行修改。TERS体积可以近似表示为焦斑面积与样品厚度乘积,因而可以推导出 Vff / Vnf ≈ Rfocus2 / RTERS2:相应地,TERS增强因子变成:
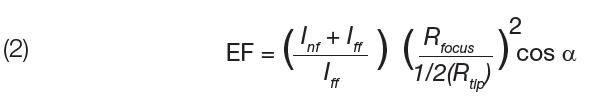
在一个实际的例子中,第一项强度比 (Inf + Iff )/Iff = 50,Rfocus=1,200 nm,Rtip=30 nm,α = 60度,第二项等于6400,第三项为 1/2,总的 TERS 增强因子 EF=2.8×105.
特别需要强调的是,TERS 增强因子的估算所依赖的几个参数,例如针尖半径、焦斑半径、近场聚焦深度、入射角以及前面提及的针尖的镜像效果等,都不是能够精确测量的。这些参数数值的误差在 20–50%,会导致对 TERS 增强的高估或低估 23。这是比较 TERS 针尖的性能时面临的一个障碍。
不可避免地,主要的误差可以看作是由于样品构成的不均匀性所致,研究人员使用各自实验室中制作的针尖,样品的密度、分子厚度都对可以重复地比较增强因子提出了挑战。要想更加精确地计算增强因子EF,人们需要更先进的针尖和样品制备协议。